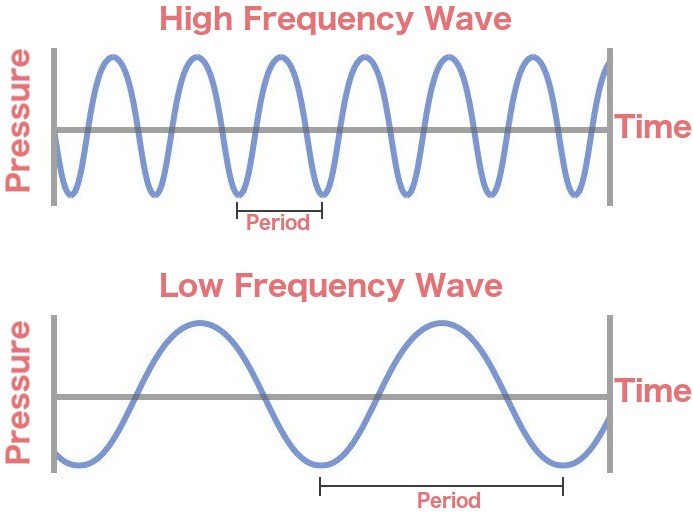
The main difference between period and frequency is in their definition. Both of these are vibration characteristics. The oscillations and vibrations of mechanical systems are important fields of study in physics. Almost all systems oscillate or vibrate freely in different ways.
Oscillation is the repetitive motion of a tool, usually in time, about a central state or between two or more distinct points. Precisely, the term vibration describes mechanical oscillation. To know more about the difference between oscillation and vibration, you can visit this link. Common examples of oscillation are a swinging pendulum, guitar strings, beating of heart, and alternating current. Even the atoms of our bodies vibrate.
Every oscillating system has something in common including force and energy. By pushing a child in a swing, a motion starts. Also by using heat, the energy of atoms increases and they vibrate. Thus, oscillations produce waves.
The characteristic that relates to all waves is periodic nature. Clearly, a few fundamental principles describe all the phenomena that prove they are more common than you thought. In each phenomenon, you see a certain pattern of movement that is repeated over and over again. Periodic motion such as a movement indicated by a guitar string or a child’s movement back and forth in a swing repeats itself at regular intervals. The time to complete a vibration or oscillation cycle is called the wave period. Frequency is a parameter equal to the number of oscillation cycles per second.
Period and Frequency Basics
The principal difference between period and frequency goes back to their definition.
Period
The period is defined as the time needed for one complete cycle of the vibration or oscillation. It refers to the time for periodic occurrence, measured in seconds per cycle. The period is usually denoted by the letter “T”.
Frequency
A wave frequency refers to the number of complete vibration cycles or oscillations taking place in one second. The unit of measurement of frequency is cycles per second or hertz (Hz). The frequency is usually indicated by the letter “f”.
Both values of time period and frequency are proportional to each other inversely. In mathematical language, period and frequency are related by the following equation:
T=\frac{1}{f}
or
f=\frac{1}{T}
Period and Frequency Natures
Period and frequency definitions show that the nature of these two parameters is different.
Period
Based on the definition of the period as the duration of completing a wave cycle in its unit, that is time, the nature of period is time.
Frequency
The frequency as the number of complete cycles occurring in unit time is a rate quantity.
Period and Frequency Schematics
In this section, we want to illustrate the concepts of period and frequency of a wave on diagrams.
Period
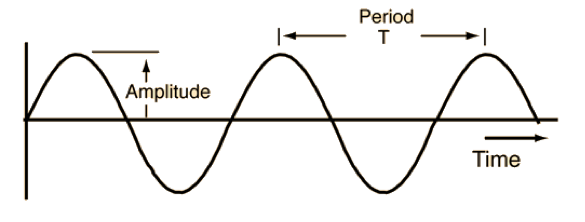
If we look at the propagation diagram of repetitive waves in terms of time, we can demonstrate the period as the distance between two successive crest of a wave (or to identical consecutive points) on the time axis.
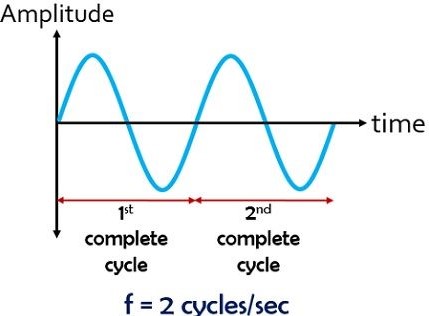
Frequency
Consider a wave that completes two full cycles per second (as shown below). Therefore, the frequency of this wave is equal to 2 Hz.
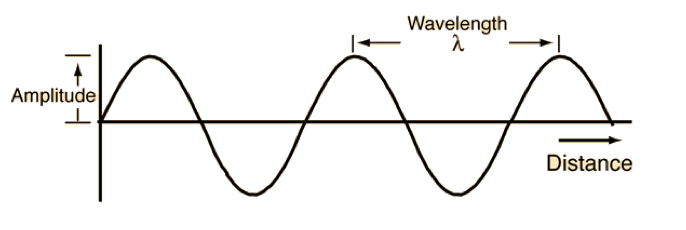
Period and Frequency Relation to the Wavelength
Consider a wave propagation with a velocity of v in m/s. The distance between two successive identical points (like two crests or troughs) on a wave diagram as a function of distance is called wavelength. It is denoted by the Greek letter “λ” and is measured in meters.
Period
The period and wavelength are related using the following equation:
T=\frac{\lambda}{v}
Frequency
The relation between frequency and wavelength is given by the equation below:
f=\frac{v}{\lambda}
It could be obvious since the period and frequency are reversely proportional to each other.
Period and Frequency Example
For a better understanding of frequency and period, look at this example. Consider a human heart, beating 75 times in one minute. If we consider a complete cycle each time, we will have to calculate the period and frequency:
Period
Using the mathematical definition of period leads to:
T=\frac{Overall\ time}{Number\ of\ cycles}=\frac{60}{75}=0.8\ (s)
Frequency
To calculate the frequency, we have:
f=\frac{Number\ of\ cycles}{Overall\ time}=\frac{1}{T}=\frac{75}{60}=1.25\ (Hz)
Period and Frequency in Physics
The concepts of period and frequency are widely used in physics, especially in the field of energy.
Period
A well-known example of the application of the period is the motion of a pendulum. The period of this motion is the time taken to travel from one side to the other and back.
An electron moving in a helical orbit is another physical example. It has a period given by:
T=\frac{2\pi m}{qB}
where m, q, and B are the electron mass, the electron charge, and the magnetic field in the region.
Frequency
Frequency is an influential parameter in engineering and science applications. It determines the rate of oscillatory and vibratory events, like mechanical vibrations, audio signals, radio waves, and light.
The wave frequency is the same as the vibration frequency creating the wave. To generate a wave with a higher frequency in a rope, you have to move the rope up and down at a higher speed. This consumes more energy, and this energy is transferred to the wave. Therefore, higher-frequency waves have more energy than lower-frequency waves with the same amplitude.
The frequency is usually presented in two forms:
Angular Frequency
The angular frequency determines the number of revolutions at the fixed time interval. The angular frequency unit is Hertz. The following equation expresses the relation between the frequency and angular frequency:
\omega =2\pi f
Where ω is the angular frequency.
Spatial Frequency
The spatial frequency depends on the spatial coordinate and is inversely proportional to the wavelength. The spatial frequency contains the characteristic of the system that works periodically in space.
Buy Equipment or Ask for a Service
By using Linquip RFQ Service, you can expect to receive quotations from various suppliers across multiple industries and regions.
Click Here to Request a Quotation From Suppliers and Service Providers
Read More on Linquip
- Difference Between Scalar and Vector Quantity
- Difference Between dB and dBm
- How to Find Frequency Statistics: Step by Step Guide
- Difference between Density and Relative Density
- What’s the Difference Between Speed and Velocity?
- Difference Between 2 Stroke and 4 Stroke
