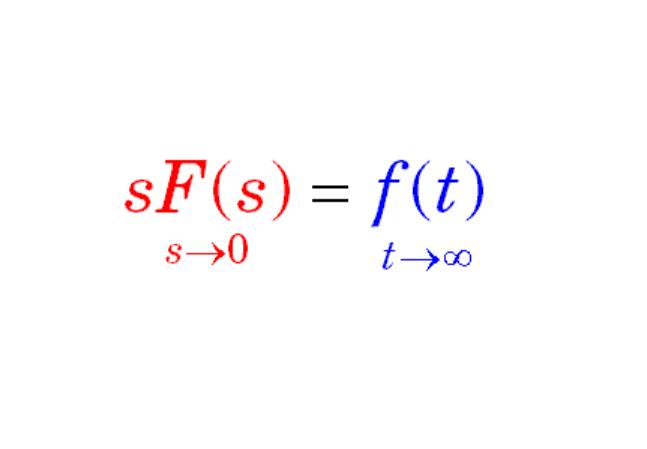What is Final Value Theorem? with Example

Table of Contents

The final value theorem (FVT) is one theorem utilized to relate frequency domain expression to the time domain behavior as time approaches infinity.

The Linquip website provides information about a variety of scientific topics. Besides researchers and those who are interested in general or specific knowledge about these topics, users and entrepreneurs who are eager to expanding their knowledge of the working principles and concepts behind industrial equipment and tools can also benefit from them. The final value theorem is a fundamental mathematical and calculating concept that is used by some specific industrial devices. You may find it helpful to visit Linquip’s page entitled “What Is Electrical Power Transmission.”

To get the most out of the Linquip platform and fully utilize its features, you must become a Linquip Expert. A Linquip expert account lets you demonstrate your expertise in the field of industrial equipment in a way that is specifically tailored to meet the needs of your industry. Would you like to be a guest writer on the Linquip website and contribute to the content of the site? It is possible to publish your content directly on Linquip’s website through the Guest Posting feature.

Mathematically, if f(t) in continuous time has Laplace transform F(s) then a final value theorem establishes situations under which

{ \lim _{ t\to \infty } f(t)=\lim _{ s\, \to \, 0 }{ sF(s) } }

Similarly, if f[k] in discrete time has Z-transform F(z) then a final value theorem establishes conditions under which

\lim _{ k\to \infty } f[k]=\lim _{ z\to 1 }{ (z-1)F(z) }

The Abelian final value theorem assumes the time domain of f(t) (or f[k]) to calculate

{ \lim _{ s\, \to \, 0 }{ sF(s) } }

On the other hand, a Tauberian final value theorem makes assumptions about the frequency-domain of F(s) to calculate

\lim _{ t\to \infty } f(t)(or{ \lim _{ k\to \infty } f[k] })

Deducing $\lim _{ t\to \infty } f(t)$

Final value theorems for obtaining $\lim _{t\to \infty }f(t)$ have usage in establishing the long-term stability of a specific system

\lim _{t\to \infty }f(t)

Standard Final Value Theorem

Suppose that every pole of F(s) is at the origin or in the open left half plane, and that F(s) has at most one pole at the origin. Then

sF(s)\to L\in { R\quad }

{ s\to 0 }

and

{ \lim _{ t\to \infty } f(t)=L }.

Final Value Theorem in Laplace Transform of the Derivative

If f(t) and f'(t) both have Laplace transforms that exist for all s>0 , and

\lim _{ t\to \infty } f(t)

and

{ \lim _{ s\, \to \, 0 }{ sF(s) } }

exists, then

{ \lim _{ t\to \infty } f(t)=\lim _{ s\, \to \, 0 }{ sF(s) } }.

Note:
Both limits must exist in order that the theorem holds. For instance, if

f(t)=\sin (t)

then

\lim _{ t\to \infty } f(t)

does not exist. However,

\lim _{ s\, \to \, 0 }{ sF(s) } =\lim _{ s\, \to \, 0 }{ \frac { s }{ s^{ 2 }+1 } } =0

Deducing ${ \lim _{ s\, \to \, 0 }{ sF(s) } }$

Another application of final value theorems for obtaining

\lim _{s\,\to \,0}{sF(s)}

In probability and statistics is to find the moments of a random variable.

Final Value Theorem in Laplace Transform of the Derivative

Suppose that all of the conditions below are satisfied:
1. $f:(0,\infty )\to { C }$ is constantly differentiable and both f and f’ have a Laplace Transform
2. f’ is completly integrable, that is ${ \int _{ 0 }^{ \infty } |f'(\tau )|\, d\tau }$ is finite
3. ${ \lim _{ t\to \infty } f(t) }$ is finite
Then

{ \lim _{ s\to 0^{ + } } sF(s)=\lim _{ t\to \infty } f(t) }.

Final Value Theorem for the Mean of a Function

Assume that ${ f:(0,\infty )\to { C } }$ be a continuous and bounded function such that the following limit exists

{ \lim _{ T\to \infty }{ \frac { 1 }{ T } } \int _{ 0 }^{ T } f(t)\, dt=\alpha \in { C } }

Then

{ \lim _{ s\, \to \, 0,\, s>0 }{ sF(s) } =\alpha }.

Examples

An Example FVT Is Applicable

For instance, for a system described by transfer function
$G(s)=\frac { 3 }{ s+4 } ,$ and so the impulse response converges to

\lim _{ t\to \infty } g(t)=\lim _{ s\to 0 } \frac { 3s }{ s+4 } =0.

The system comes to zero after being disturbed by a short impulse. Nevertheless, the Laplace transform of the unit step response is

H(s)=\frac { 1 }{ s } \frac { 3 }{ s+4 }

Thus the step response converges to

\lim _{ t\to \infty } h(t)=\lim _{ s\to 0 } \frac { s }{ s } \frac { 3 }{ s+4 } =\frac { 3 }{ 4 } =0.75

Thus, a zero-state system will follow an exponential rise to a final value of 0.75.

An Example FVT Is Not Applicable

For a system determined by the transfer function

H(s)=\frac { 16 }{ s^{ 2 }+16 } ,

the final value theorem seems to predict the final value of the step response to be one and the final value of the impulse response to be zero. Though, the time-domain limit does not exist, and so the final value theorem forecasts are not valid.

Both the step response and impulse response oscillate, and (in this special case) the final value theorem determines the average values where the responses oscillate.
There are two analyses performed in Control theory that confirm valid results for the Final Value Theorem:
All non-zero roots in the denominator of H(s) must contain negative real parts.
H(s) must not possess more than one pole at the origin.
Rule 1 was not satisfied in this case, in that the roots of the denominator are $0+j4$ and $0-j4.$